SpringBoot使用prometheus监控
本文共 3623 字,大约阅读时间需要 12 分钟。
本文介绍SpringBoot如何使用Prometheus配合Grafana监控。
1.关于Prometheus
Prometheus是一个根据应用的metrics来进行监控的开源工具。相信很多工程都在使用它来进行监控,有关详细介绍可以查看官网:。
2.有关Grafana
Grafana是一个开源监控利器,如图所示。
从图中就可以看出来,使用Grafana监控很高大上,提供了很多可视化的图标。
官网地址:
3.SpringBoot使用Prometheus
3.1 依赖内容
在SpringBoot中使用Prometheus其实很简单,不需要配置太多的东西,在pom文件中加入依赖,完整内容如下所示。
4.0.0 org.springframework.boot spring-boot-starter-parent 2.1.3.RELEASE com.dalaoyang springboot2_prometheus 0.0.1-SNAPSHOT springboot2_prometheus springboot2_prometheus 1.8 org.springframework.boot spring-boot-starter-actuator org.springframework.boot spring-boot-starter-web org.springframework.boot spring-boot-starter-test test io.micrometer micrometer-registry-prometheus 1.1.3 org.springframework.boot spring-boot-maven-plugin
3.2 配置文件
配置文件中加入配置,这里就只进行一些简单配置,management.metrics.tags.application属性是本文配合Grafana的Dashboard设置的,如下所示:
spring.application.name=springboot_prometheusmanagement.endpoints.web.exposure.include=*management.metrics.tags.application=${spring.application.name} 3.3 设置application
修改启动类,如下所示.
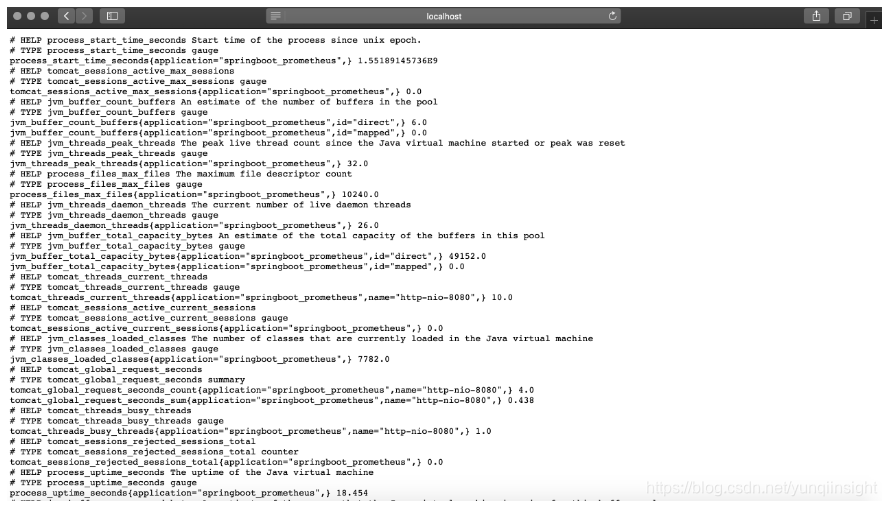
@SpringBootApplicationpublic class Springboot2PrometheusApplication { public static void main(String[] args) { SpringApplication.run(Springboot2PrometheusApplication.class, args); } @Bean MeterRegistryCustomizer configurer( @Value("${spring.application.name}") String applicationName) { return (registry) -> registry.config().commonTags("application", applicationName); }} SpringBoot项目到这里就配置完成了,启动项目,访问,如图所示,可以看到一些度量指标。
4.Prometheus配置
4.1 配置应用
在prometheus配置监控我们的SpringBoot应用,完整配置如下所示。
# my global configglobal: scrape_interval: 15s # Set the scrape interval to every 15 seconds. Default is every 1 minute. evaluation_interval: 15s # Evaluate rules every 15 seconds. The default is every 1 minute. # scrape_timeout is set to the global default (10s).# Alertmanager configurationalerting: alertmanagers: - static_configs: - targets: # - alertmanager:9093# Load rules once and periodically evaluate them according to the global 'evaluation_interval'.rule_files: # - "first_rules.yml" # - "second_rules.yml"# A scrape configuration containing exactly one endpoint to scrape:# Here it's Prometheus itself.scrape_configs: - job_name: 'prometheus' static_configs: - targets: ['127.0.0.1:9090']###以下内容为SpringBoot应用配置 - job_name: 'springboot_prometheus' scrape_interval: 5s metrics_path: '/actuator/prometheus' static_configs: - targets: ['127.0.0.1:8080']
4.2 启动Prometheus
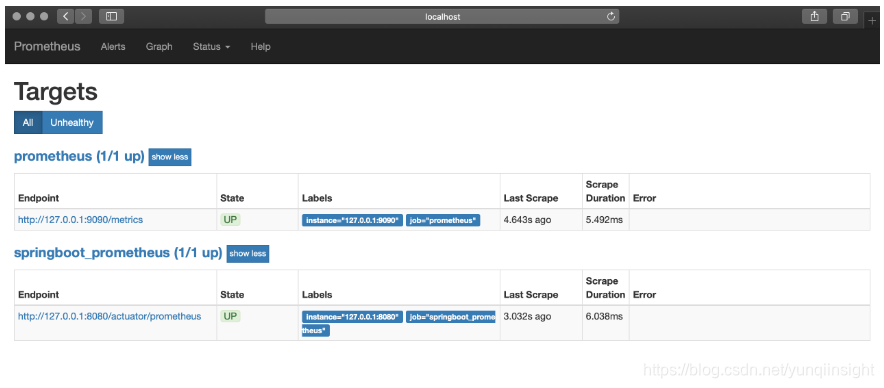
启动Prometheus,浏览器访问,查看Prometheus页面,如图所示。
点击如图所示位置,可以查看Prometheus监控的应用。
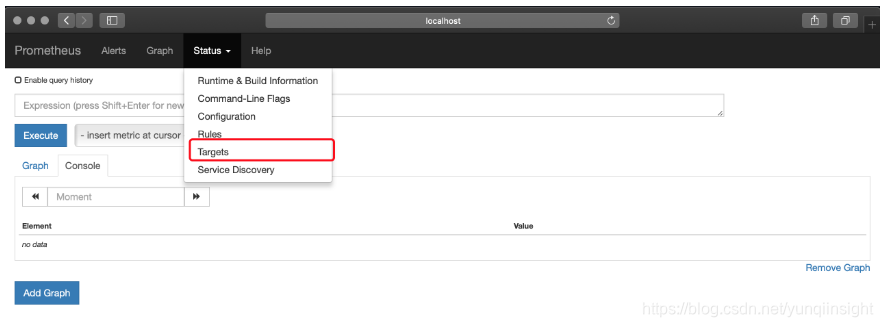
列表中UP的页面为存活的实例,如图所示。
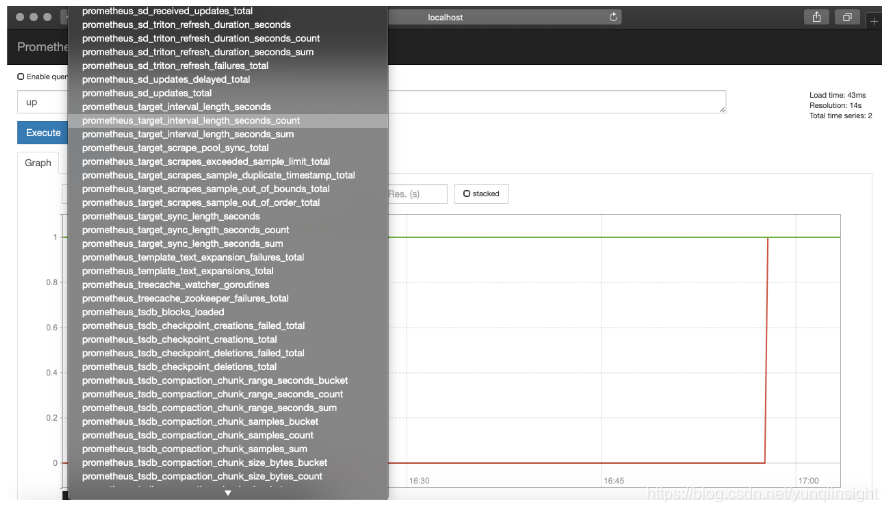
也可以查看很多指数,如下所示。
5.Grafana配置
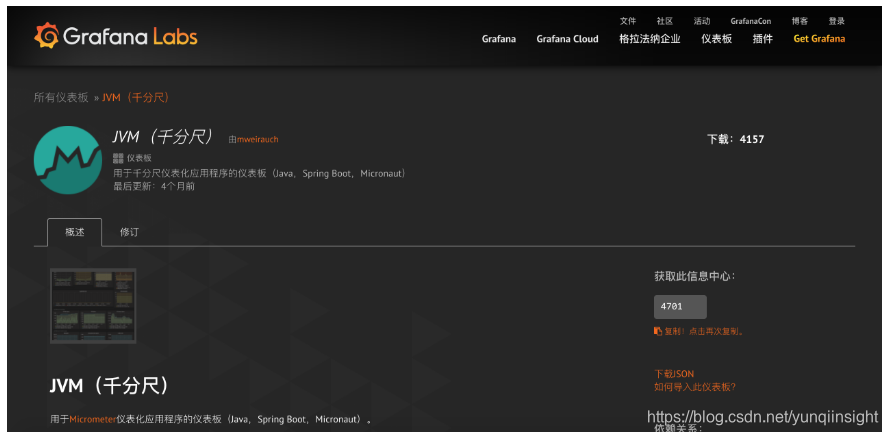
启动Grafana,配置Prometheus数据源,这里以ID是4701的Doshboard为例(地址:)如图。
在Grafana内点击如图所示import按钮
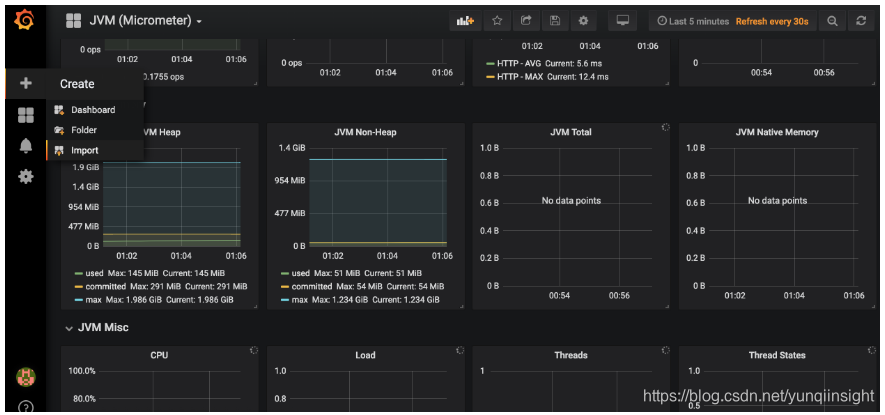
在如图所示位置填写4701,然后点击load。
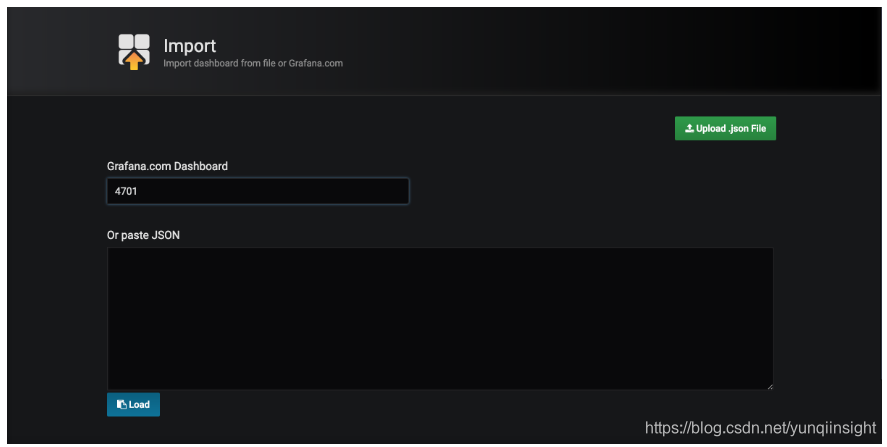
接下来导入Doshboard。
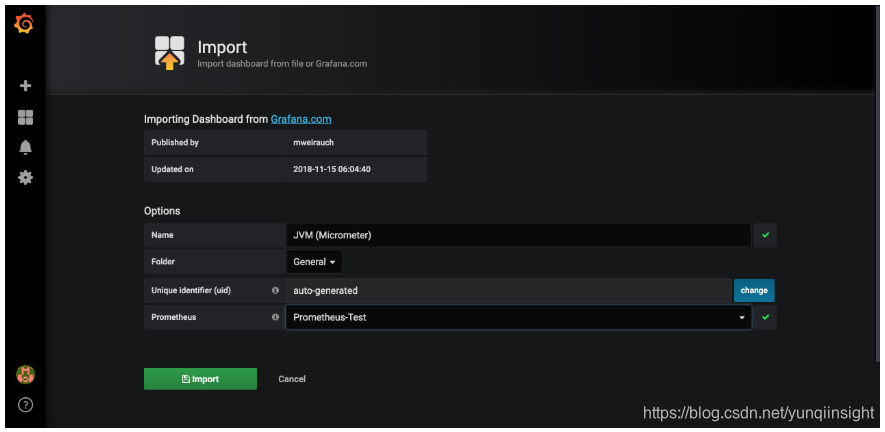
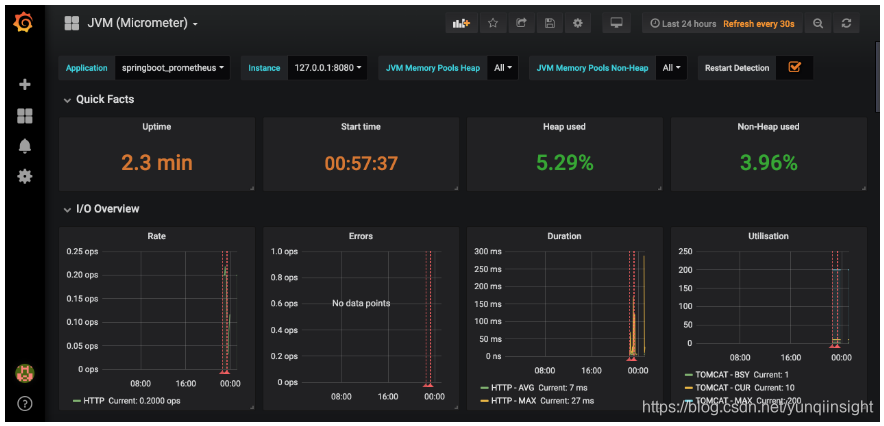
导入后就可以看到我们的SpringBoot项目对应的指标图表了,如图。
6.源码
源码地址:
本文为云栖社区原创内容,未经允许不得转载。
你可能感兴趣的文章
MYSQL一直显示正在启动
查看>>
MySQL一站到底!华为首发MySQL进阶宝典,基础+优化+源码+架构+实战五飞
查看>>
MySQL万字总结!超详细!
查看>>
Mysql下载以及安装(新手入门,超详细)
查看>>
MySQL不会性能调优?看看这份清华架构师编写的MySQL性能优化手册吧
查看>>
MySQL不同字符集及排序规则详解:业务场景下的最佳选
查看>>
Mysql不同官方版本对比
查看>>
MySQL与Informix数据库中的同义表创建:深入解析与比较
查看>>
mysql与mem_细说 MySQL 之 MEM_ROOT
查看>>
MySQL与Oracle的数据迁移注意事项,另附转换工具链接
查看>>
mysql丢失更新问题
查看>>
MySQL两千万数据优化&迁移
查看>>
MySql中 delimiter 详解
查看>>
MYSQL中 find_in_set() 函数用法详解
查看>>
MySQL中auto_increment有什么作用?(IT枫斗者)
查看>>
MySQL中B+Tree索引原理
查看>>
mysql中cast() 和convert()的用法讲解
查看>>
mysql中datetime与timestamp类型有什么区别
查看>>
MySQL中DQL语言的执行顺序
查看>>
mysql中floor函数的作用是什么?
查看>>